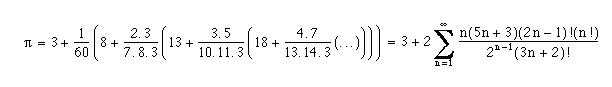L'approche qualité avec OCaml

Notre module Big_nat n'implémentera que les opérations sur les grands entiers positifs ou nuls.

module Big_nat = struct
  ...
end;;

Pour ce qui est de la base du système de numération, elle dépendra de la longueur du mot machine :

let base =
  match Sys.word_size with
  | 32 -> 10000 
  | 64 -> 1000000000 
  | _  -> 10;;

Pour ce qui est de la représentation des nombres, nous avons deux choix possibles :

• ou bien le type int list ;
• ou bien le type int array.

L'inconvénient majeur du type int list c'est qu'on ne peut le parcourir que dans un sens, or :

• l'addition de deux entiers nous impose de progresser des digits de poids faible vers les digits de poids fort ;
• l'inégalité de deux entiers nous impose de progresser des digits de poids fort vers les digits de poids faible.

C'est ainsi que notre objectif d'une implémentation efficace nous pousse vers le type int array, avec toutes les vicissitudes du style impératif que cela implique. Nous choisissons néanmoins cette option et nous définissons le type Big_nat.big_nat ainsi que son abréviation Big_nat.t :

type big_nat = int array;;
type t = big_nat;;

Dans la foulée nous introduisons deux constantes pas forcément inutiles :

let zero_big = ([|0|]: big_nat)
and unit_big = ([|1|]: big_nat)
;;

Il reste une dernière chose à régler : pour simplifier nos fonctions, nous devons assurer l'unicité de la représentation de chaque entier. Pour cela nous décidons que le digit de poids fort sera toujours strictement supérieur à zéro. La seule et unique exception à cette règle sera le nombre zero_big défini ci-dessus.

À ce stade nous pouvons implémenter un constructeur élémentaire pour notre type big_nat :

let big_of_int n =
  assert (0 <= n && n < base * base);
  if n < base then ([|n|]: big_nat)
  else ([|n / base;n mod base|]: big_nat);;

Essai sur une plateforme 32 bits :

# base;;
- : int = 10000
# big_of_int 1500123;;
- : big_nat = [|150; 123|]

Comme vous pouvez le constater, un zéro significatif a disparu à l'affichage.

Afin d'assurer la manipulation efficace des importantes quantités d'int que pourront contenir nos grands entiers, nous aurons besoin du support de trois fonctions supplémentaires du module Array :

• Array.copy a renvoie une nouvelle copie du tableau a ;
• Array.sub a start len renvoie un nouveau tableau de longueur len, qui contient len éléments du tableau a, de l'indice start à l'indice start + len - 1, en cas de dépassement des bornes l'erreur invalid_arg "Array.sub" est déclenchée ;
• Array.blit a1 i1 a2 i2 len copie len éléments du tableau a1 vers le tableau a2, la lecture commence à l'indice i1 du tableau a1, l'écriture commence à l'indice i2 du tableau a2, en cas de dépassement des bornes l'erreur invalid_arg "Array.blit" est déclenchée, Array.blit autorise la copie à l'intérieur d'un même tableau, même dans les cas où il y a recouvrement de l'intervalle source et de l'intervalle destination.

Quant à l'affichage d'un big_nat, il ne nécessitera qu'une seule nouvelle fonction du module Array :

• Array.iteri f a applique f i a.(i) pour tous les éléments d'indice i de 0 à Array.length a - 1

let print_big (a: big_nat) =
  let print i n =
    if i=0 then print_int n
    else if base=10 then print_int n
    else if base=10000 then Printf.printf "%04d" n
    else Printf.printf "%09d" n
  in Array.iteri print a;;

Essai sur une plateforme 32 bits :

# base;;
- : int = 10000
# print_big [|150;123|];;
1500123- : unit = ()

Comme vous pouvez le constater, un zéro significatif a été révélé à l'affichage.

Pour implémenter l'addition nous allons utiliser une fonction auxiliaire add_big.
Si a contient au moins autant de digits que b alors la fonction add_big a b effectue l'assignation a := a + b.

Pour ce faire :

• il faut additionner tous les digits de b aux digits de poids faible de a ;
• une fois les digits de b épuisés il faut éventuellement propager une retenue dans les digits de poids fort restants dans a ;
• une fois les digits de a épuisés, une retenue éventuelle provoque un débordement qui oblige à réallouer une copie du tableau a ;
• finalement le tableau a initial (ou bien sa copie) est retourné en résultat.

Les deux premiers points font l'objet des deux boucles while qui constituent l'essentiel de la fonction add_big.
Le troisième point fait l'objet de la dernière branche else begin ... end.
Enfin le quatrième et dernier point est réalisé par l'expression finale !result.

let add_big (a: big_nat) (b: big_nat) =
  assert (Array.length a >= Array.length b);
  let result = ref a
  and carry  = ref 0
  and i = ref (Array.length a - 1)
  and j = ref (Array.length b - 1)
  in begin
    while !j >= 0 do
      let d = a.(!i) + b.(!j) + !carry
      in if d < base then begin
        carry := 0; a.(!i) <- d 
      end else begin
        carry := 1; a.(!i) <- d - base
      end;
      decr i; decr j; 
    done;
    while !carry > 0 do
      if !i >= 0 then begin
        let d = a.(!i) + !carry
        in if d < base then begin
          carry := 0; a.(!i) <- d 
        end else begin
          a.(!i) <- d - base
        end;
        decr i;
      end else begin
        result := Array.make (Array.length a + 1) 0;
        Array.blit a 0 !result 1 (Array.length a);
        !result.(0) <- 1; carry := 0;
      end;
    done;
    !result
  end;;

La fonction add_big sert de support pour la fonction sum_big qui effectue l'addition générale.
Pour cela il suffit de copier le tableau a après avoir éventuellement inversé les arguments a et b, afin que a contienne toujours plus de digits que b :

let sum_big (a: big_nat) (b: big_nat) =
  if Array.length a >= Array.length b then
    add_big (Array.copy a) b
  else 
    add_big (Array.copy b) a
  ;;

Pour effectuer la comparaison de a et b il y a trois cas à traiter :

• ou bien a comporte moins de digits que b alors a est plus petit que b ;
• ou bien a comporte plus de digits que b alors a est plus grand que b ;
• ou bien a et b comportent le même nombre de digits.

Dans le troisième cas, le résultat est déterminé par la première paire de digits non égaux, en progressant des digits de poids fort vers les digits de poids faible. La transcription en code OCaml ne pose pas de difficulté particulière :

let compare_big (a: big_nat) (b: big_nat) =
  if Array.length a < Array.length b then -1
  else if Array.length a > Array.length b then 1
  else
    let i = ref 0 in
    begin
      while !i < Array.length a && a.(!i) = b.(!i) do
        incr i;
      done;
      if !i = Array.length a then 0
      else if a.(!i) > b.(!i) then 1
      else -1
    end;;

Au passage, on ne se prive pas d'implémenter le minimum et le maximum :

let min_big (a: big_nat) (b: big_nat) =
  if compare_big a b < 0 then a else b;;

let max_big (a: big_nat) (b: big_nat) =
  if compare_big a b > 0 then a else b;;

La soustraction présente beaucoup de points communs avec l'addition, on reconnaîtra notamment :

• une même fonction auxiliaire, ici sub_big a b ;
• les deux mêmes boucles while qui constituent l'essentiel de la fonction sub_big a b ;
• une même copie éventuelle du tableau a, destinée ici à éliminer les zéros en tête ;
• la même expression finale !result qui renvoie a ou bien sa copie ;
• la même opération généralisée, ici diff_big a b.

Là où la soustraction est un peu plus exigente que l'addition, c'est dans sa précondition. Cette fois il ne suffira plus que a ait au moins autant de digits que b, pour ne pas sortir du domaine des entiers naturels il faudra impérativement que a soit supérieur ou égal à b.

let sub_big (a: big_nat) (b: big_nat) =
  assert (compare_big a b >= 0);
  let result = ref a
  and carry  = ref 0
  and i = ref (Array.length a - 1)
  and j = ref (Array.length b - 1)
  in begin
    while !j >= 0 do
      let d = a.(!i) - b.(!j) - !carry
      in if d >= 0 then begin
        carry := 0; a.(!i) <- d 
      end else begin
        carry := 1; a.(!i) <- d + base
      end;
      decr i; decr j; 
    done;
    while !carry > 0 do
      let d = a.(!i) - !carry
      in if d >= 0 then begin
        carry := 0; a.(!i) <- d 
      end else begin
        a.(!i) <- d + base
      end;
      decr i;
    done;
    if !i < 0 then begin
      i := 0; j := Array.length a - 1;
      while a.(!i) = 0 && !i < !j  do incr i; done;
      if !i >= 0 then result := Array.sub a !i (Array.length a - !i);
    end;  
    !result
  end;;


let diff_big (a: big_nat) (b: big_nat) =
  assert (compare_big a b >= 0);
  sub_big (Array.copy a) b;;

Pour la multiplication nous décomposons l'opération en trois étapes :

• d'abord la multiplication d'un big_nat par un int strictement inférieur à base ;
• ensuite le décalage à gauche d'un big_nat ;
• enfin la multiplication d'un big_nat par un big_nat selon la méthode enseignée à l'école primaire.

Première étape.
Multiplier un big_nat par un int strictement inférieur à base.
Il s'agit essentiellement d'une boucle for qui propage la retenue des digits de poids faible vers les digits de poids fort.
Le if final est destiné à éliminer un éventuel zéro en tête.

let scale_up_big (a: big_nat) n =
  assert (0 <= n && n < base);
  if n = 0 then zero_big
  else 
    let accu  = ref 0 
    and carry = ref 0
    and result: big_nat = Array.make (Array.length a + 1) 0
    in begin
      for i = (Array.length a) downto 1 do
        accu := a.(i-1) * n + !carry; 
        result.(i) <- !accu mod base; carry := !accu/base
      done;
      result.(0) <- !carry;
      if !carry = 0 then
        (Array.sub result 1 (Array.length a): big_nat)
      else
        result  
    end;;

Deuxième étape.
Décaler un big_nat de n digits à gauche.
On fait une copie calée au début d'un nouveau tableau contenant n digits supplémentaires initialisés à zéro.

let shift_big (a: big_nat) n =
  assert (n >= 0);
  if a = zero_big then zero_big
  else
    let result: big_nat = Array.make (Array.length a + n) 0
    in begin
      Array.blit a 0 result 0 (Array.length a);
      result
    end;;

Troisième étape.
Comme à l'école primaire, les digits de b, du poids faible au poids fort, servent de facteur pour scale_up_big a, à chaque digit on décale le résultat d'un digit de plus, puis on somme le tout.

let long_mult_big (a: big_nat) (b: big_nat) =
  let i = ref 0
  and j = ref (Array.length b-1) in
  let result = ref (shift_big (scale_up_big a b.(!i)) !j) 
  in begin
    while !j > 0 do
      incr i; decr j;
      result := add_big !result (shift_big (scale_up_big a b.(!i)) !j)
    done;  
    !result
  end;;

Nous allons maintenant réaliser un produit raisonnablement efficace de deux entiers naturels p et q.

Supposons que p et q aient chacun 2n digits.
On peut alors décomposer p et q en les divisant par basen, comme ceci :

p = a.basen + b ;
q = c.basen + d.

Ce qui nous donne la valeur du produit pq :

pq = ac.base2n + (ad + bc).basen + bd.

C'est-à-dire que quand la taille des nombres double (passe de n à 2n) il faut faire 4 fois plus de multiplications, plus précisément il faut faire les 4 produits ac, ad, bc et bd. C'est exactement ce qui explique la lenteur de la multiplication, le doublement de la taille des opérandes entraîne un quadruplement du temps de calcul.
L'idée ingénieuse de Karatsuba (reprise et popularisée par Knuth) consiste à remarquer l'égalité suivante :

ad + bc = (a + b)(c + d) - ac - bd.

Du coup, en remplaçant ad + bc, la valeur du produit pq devient :

pq = ac.base2n + [(a + b)(c + d) - ac - bd].basen + bd.

Algorithmiquement, cette nouvelle égalité est bien plus intéressante que la précédente, car elle nous dit qu'un doublement de la taille des opérandes n'entraîne qu'un triplement du temps de calcul.
En effet, énumérons les produits à effectuer :

• il y a toujours le produit ac ;
• il y a toujours le produit bd ;
• inconvénient : il y a un nouveau produit (a + b)(c + d) ;
• avantage : il n'y a plus les deux produits ad et bc.

Évidemment, l'avantage vaut le double de l'inconvénient, car il ne reste plus que 3 produits à effectuer au lieu de 4 !

Le code qui effectue cette nouvelle multiplication se compose de deux fonctions.
La première est array_sub qui extrait une portion des digits d'un big_nat en retirant les éventuels zéros en tête :

let array_sub (a: big_nat) start len = 
  let i = ref start and n = ref len in
  while a.(!i)=0 && !n > 1 do
    incr i; decr n;
  done;
  (Array.sub a !i !n : big_nat);;

La deuxième est mult_big qui implémente la multiplication Karatsuba, avec trois améliorations notables :

• la généralisation à un nombre quelconque de digits, pas seulement les puissances de 2 ;
• le recours à long_mult_big lorsqu'elle est plus efficace (empiriquement, en dessous de 20 à 30 digits) ;
• une formule simplifiée dans le cas où q est au moins 2 fois plus court que p.

let karatsuba_threshold = 20;;

let rec mult_big (a: big_nat) (b: big_nat) =
  if Array.length a < Array.length b then
    mult_big b a
  else if Array.length b < karatsuba_threshold then
    long_mult_big a b
  else 
    karatsuba_big a b
and karatsuba_big (p: big_nat) (q: big_nat) =
  assert (Array.length p >= Array.length q);
  let len_p = Array.length p  in
  let len_q = Array.length q  in
  let     n = len_p / 2       in
  let     a = array_sub p 0 (len_p - n)  in
  let     b = array_sub p (len_p - n) n  in
  if len_q > n then  
    let      c = array_sub q 0 (len_q - n)  in
    let      d = array_sub q (len_q - n) n  in
    let     ac = mult_big a c  in
    let     bd = mult_big b d  in
    let  ad_bc = sub_big (sub_big (mult_big (sum_big a b) (sum_big c d)) ac) bd
    in
    add_big (add_big (shift_big ac (2*n)) (shift_big ad_bc n)) bd
  else  
    let     aq = mult_big a q in
    let     bq = mult_big b q in
    add_big (shift_big aq n) bq
    ;;

La multiplication apporte avec elle son lot de nouvelles opérations.
Grâce à la complexité sub-quadradrique de la multiplication Karatsuba, ces opérations sont plus efficaces qu'avec une implémentation naïve.

Le carré :

let square_big (a: big_nat) = mult_big a a;;

La puissance entière, implémentée de façon dichotomique :

let rec power_big (a: big_nat) n =
  assert (n >= 0);
  if n=0 then unit_big
  else if n=1 then a
  else
    let b = power_big a (n/2) in
    if (n mod 2 = 0) then mult_big b b 
    else mult_big (mult_big b b) a;;

La permutation de p éléments parmi n, elle aussi implémentée de façon dichotomique :

let permutation_big n p =
  assert(0 <= p && p <= n);
  let rec product a b =
    if a = b then
      big_of_int a
    else if a + 1 = b then
      big_of_int (a * b)
    else 
      let ab2 = (a + b) / 2 in
      mult_big (product a ab2) (product (ab2+1) b)
  in
    if p = 0 then unit_big else product (n - p + 1) n;;

Enfin, la factorielle qui n'est que la permutation de n éléments parmi n :

let factorial_big n =
  assert(n >= 0);
  permutation_big n n;;

Pour la division nous décomposons l'opération en deux étapes :

• d'abord la division d'un big_nat par un int strictement inférieur à base² ;
• ensuite la division d'un big_nat par un big_nat selon l'algorithme de Burnikel et Ziegler, que nous présenterons sans le justifier.

Première étape.

Diviser un big_nat par un int inférieur à base².
Il s'agit essentiellement d'une boucle for qui propage la retenue des digits de poids fort vers les digits de poids faible.
Comme à l'habitude, le if final est l'étape d'élimination de l'éventuel zéro en tête.

let scale_down_big (a: big_nat) n =
  assert (0 < n && n < base * base);
  let last  = Array.length a - 1 in
  let accu  = ref 0 
  and carry = ref 0
  and result: big_nat = Array.copy a
  in begin
    for i = 0 to last do
      accu := a.(i) + !carry * base; 
      result.(i) <- !accu/n; carry := !accu mod n
    done;
    if (result.(0) = 0) && (last > 0) then
      (array_sub result 1 last: big_nat),!carry
    else
      result,!carry
  end;;

Deuxième étape.

Remarquons qu'un entier inférieur à base² c'est exactement le nombre que peut stocker un big_nat de deux digits.

Une fois acquise la division par un nombre de deux digits, l'algorithme publié en 2000 par Michel Quercia et Paul Zimmermann, et qui est une amélioration d'une idée originale de Burnikel et Ziegler, permet le passage à une division quelconque. Il utilise une méthode dichotomique qui apporte à la division l'équivalent de ce que la méthode Karatsuba apporte à la multiplication.
La description de l'algorithme est suivie d'un petit commentaire sur le respect du domaine de définition, puis l'implémentation s'ensuit naturellement, la notation restant assez proche de la spécification mathématique tout en réutilisant nombre de fonctions auxiliaires introduites pour la mutiplication.

Soit n = (le nombre de digits de b - 1) / 2
Ou bien n = 0 :

diviser a par b à l'aide de la fonction scale_down_big ;

Ou bien n > 0 :

décomposer a selon le binôme a = a1.basen + a0
si a1 >= b :

• diviser récursivement a1 par b selon l'égalité a1 = b.q1 + r1
• diviser récursivement r1.basen + a0 par b selon l'égalité r1.basen + a0 = b.q0 + r0
• alors r = r0 et q = q1.basen + q0 ;

si a1 < b :

• décomposer b selon le binôme b = b1.basen + b0 ,
• diviser récursivement a1 par b1 selon l'égalité a1 = b1.q1 + r1,
• soit x = a0 + r1.basen - b0.q1,
• si x >= 0 alors r = x et q = q1 sinon r = b + x et q = q1 - 1.

Dans le cas où a1 < b, avec nos entiers positifs on ne pourra pas directement calculer x, il faudra comparer a0 + r1.basen avec b0.q1, et le reste vaudra, suivant le signe de x, ou bien x ou bien b -(-x).

let rec burnikel_ziegler_big (a: big_nat) (b: big_nat) =
  if Array.length b <= 2 then
    let b2 = if Array.length b < 2 then b.(0) else b.(0)*base + b.(1) in
    let q,r = scale_down_big a b2
    in  q,big_of_int r
  else    
    let   len_a = Array.length a               in
    let   len_b = Array.length b               in
    let       n = (len_b - 1) / 2              in
    let      a0 = array_sub a (len_a - n) n    in
    let      a1 = array_sub a 0 (len_a - n)    in
    if compare_big a1 b >= 0 then
      let q1,r1 = burnikel_ziegler_big a1 b    in
      let q0,r0 = burnikel_ziegler_big (sum_big (shift_big r1 n) a0) b
      in  sum_big (shift_big q1 n) q0,r0
    else
      let    b0 = array_sub b (len_b - n) n    in
      let    b1 = array_sub b 0 (len_b - n)    in
      let q1,r1 = burnikel_ziegler_big a1 b1   in
      let a0_r1 = sum_big (shift_big r1 n) a0  in
      let b0_q1 = mult_big b0 q1               in
      if compare_big a0_r1 b0_q1 >= 0 then
        let plus_x = diff_big a0_r1 b0_q1
        in  q1,plus_x
      else
        let minus_x = diff_big b0_q1 a0_r1 in
        diff_big q1 unit_big, diff_big b minus_x;;

La dernière touche c'est la fonction quomod_big qui enveloppe burnikel_ziegler_big dans une interface plus commune, en traitant notamment le cas particulier de la division par zéro :

let quomod_big (a: big_nat) (b: big_nat) =
  if b = zero_big then raise Division_by_zero
  else if compare_big a b < 0 then zero_big,a
  else burnikel_ziegler_big a b;;

Et pour finir, voici un calcul efficace des coefficients binomiaux :

La formule ci-dessus, due à William Gosper, possède le double avantage :

• de ne faire intervenir que les quatre opérations élémentaires ;
• d'admettre une implémentation en goutte-à-goutte, l'affichage démarre immédiatement, les décimales s'affichent une à une, de plus nous n'avons pas à sélectionner une précision maximale par avance.

Comme souvent dans les formules un peu complexes, mieux vaut commencer par définir quelques abréviations afin d'alléger la notation :

let add a b  =
    if Array.length a >= Array.length b then Big_nat.add_big a b
    else Big_nat.add_big b a
and sub      = Big_nat.sub_big
and mult     = Big_nat.mult_big
and div a b  = let q,r = Big_nat.quomod_big a b in q
and add_int  n a = Big_nat.sum_big a [|n|]
and sub_int  n a = Big_nat.sub_big a [|n|]
and mult_int n a = Big_nat.scale_up_big a n
and big_int  = Big_nat.big_of_int
and int_of n = match n with [|n|] -> n | _ -> assert false
;;

L'implémentation en goutte-à-goutte est due à Jeremy Gibbons, il s'agit d'une simple boucle, chaque itération affichant une décimale supplémentaire :

let pi () =
  let rec g q r t i =
    let i3 = mult_int 3 i in
    let u = mult_int 3 (mult (add_int 1 i3) (add_int 2 i3))
    and y = int_of (div (add (mult q (sub_int 12 (mult_int 27 i))) (mult_int 5 r)) (mult_int 5 t)) 
    in begin
      print_int y;
      flush stdout;
      g
      (mult_int 10 (mult q (mult i (sub_int 1 (mult_int 2 i)))))
      (mult_int 10 (mult u (sub (add (mult q (sub_int 2 (mult_int 5 i))) r) (mult_int y t))))
      (mult t u)
      (add_int 1 i);
      ()
    end
  in g (big_int 1) (big_int 180) (big_int 60) (big_int 2);;

Comme on ne fait aucun passage à la ligne, on est obligé de forcer l'affichage à l'aide de flush stdout.

Prêt ? Partez :

pi ();;

Pour interrompre le calcul dans OCamlWinPlus il faut invoquer le menu Workspace/Interrupt.
Pour interrompre le calcul dans une console de commandes il faut envoyer un signal d'interruption (le plus souvent en appuyant sur Ctrl+C).