L'approche qualité avec OCaml

À la lumière de ses spécifications on peut écarter l'idée d'implémenter notre tableau extensible à l'aide d'un classique array, quelle que soit la manière de contourner l'absence de bornes elle nous conduirait à une perte d'espace insupportable dans le cas général. Le type array n'est définitivement adapté qu'à des indices raisonnablement consécutifs.

L'arbre AVL (Adelson-Velskii-Landis) représente une alternative plus crédible :

• il n'impose aucune borne sur la clé ;
• il est optimum en espace, une cellule pour un élément ;
• les opérations élémentaires sont exécutées en temps logarithmique.

Malheureusement l'arbre AVL est délicat à coder, c'est un TAD qui n'impose qu'une relation d'ordre total sur les clés, il est en quelque sorte trop général pour ce que nous voulons faire. Au lieu d'un AVL nous allons utiliser un autre arbre binaire, moins sophistiqué, plus spécifique aux clés entières et au moins aussi performant.

L'idée essentielle de notre TAD c'est une bijection entre ℕ et les chemins dans un arbre binaire :

• un entier en base 2 est une liste de digits (0 ou 1) ;
• un chemin dans un arbre binaire est une liste de directions (gauche ou droite).

Or, dans un arbre binaire, partant de la racine, il y a bijection entre les chemins et les nœuds.
Il y a donc une bijection entre ℕ et les nœuds, ou autrement dit, puisqu'un dictionnaire n'est rien d'autre qu'une bijection entre les clés et les articles, nous avons trouvé la structure qui sied à nos besoins.

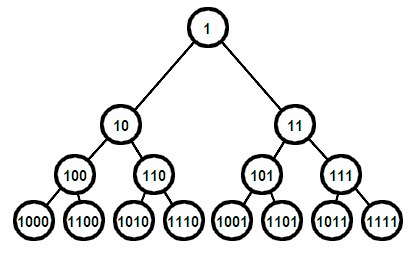
Nous obtiendrons une extension à ℤ par simple dédoublement :

• un premier arbre de Braun contiendra les clés positives ou nulles ;
• un second arbre de Braun contiendra les clés strictement négatives.

Quelle interface souhaitons-nous ?

Hé bien le client d'un tel module est en droit d'attendre :

• un constructeur make ;
• les traditionnels accesseurs set et get ;
• les itérateurs classiques iter, exists, for_all et filter ;
• un itérateur plus général fold ;
• les variantes avec indice, à savoir iteri, foldi et mapi ;
• le foncteur map ;
• to_list, la fonction de conversion en une liste ;
• to_alist, la fonction de conversion en une liste d'association.

Afin de cacher les détails d'implémentation au client d'un module, on peut mettre l'interface du module dans un fichier séparé *.mli, voici par exemple à quoi ressemblerait notre fichier Vector.mli :

module Vector :
  sig
    type 'a t
    val make : 'a -> 'a t
    val get : 'a t -> int -> 'a
    val set : 'a t -> int -> 'a -> unit
    val iter : ('a -> unit) -> 'a t -> unit
    val exists : ('a -> bool) -> 'a t -> bool
    val for_all : ('a -> bool) -> 'a t -> bool
    val filter : ('a t -> bool) -> 'a t -> 'a list
    val map : ('a -> 'b) -> 'a t -> 'b t
    val fold : ('a -> 'b -> 'b) -> 'b -> 'a t -> 'b
    val iteri : (int -> 'a -> unit) -> 'a t -> unit
    val foldi : (int -> 'a -> 'b -> 'b) -> 'b -> 'a t -> 'b
    val mapi : (int -> 'a -> 'b) -> 'a t -> 'b t
    val to_list : 'a t -> 'a list
    val to_alist : 'a t -> (int * 'a) list
  end

Tant que le fichier *.mli est présent il ne sera pas possible au client de savoir, par exemple, comment est implémenté le type 'a Vector.t

Le bémol c'est que, contrairement à notre habitude, il nous faut donner le type de toutes les fonctions, ou plus exactement de toutes celles qui sont exportées. Alors on n'y perd aucune sécurité puisque l'implémentation sera systématiquement comparée à l'interface déclarée, mais n'y perd-on pas un peu de notre confort ?
Hé bien pas vraiment, car il faut bien l'avouer on procède souvent à rebours, n'oublions pas que la signature est le type d'un module. Il suffit donc de coller la source du module dans l'interpréteur et celui-ci nous affiche sa signature, il ne reste plus qu'à effacer les informations 'compromettantes' pour obtenir une interface respectable.
Bien sûr, on prendra soin de rester soupçonneux et de vérifier avec attention que le type inféré correspond bien à l'idée intuitive que l'on se fait de chaque opération.

Notre arbre de Braun est mutable, nous aurions pu choisir une implémentation persistante, mais ça ne faisait pas partie de nos exigences de départ. Persistant ou pas les algorithmes sont tout à fait comparables et notre implémentation suffira bien à illustrer le parcours sur une structure de données non triviale.

    type 'a vector =
      | Leaf
      | Node of 'a node
    and 'a node =
      {mutable left: 'a vector; mutable item: 'a; mutable right: 'a vector}

Nous avons besoin de deux arbres de Braun (un pour les indices positifs, un pour les indices négatifs) ainsi que d'un article par défaut :

    type 'a t =
      {mutable plus: 'a vector; mutable minus: 'a vector; default: 'a}

Tout indice qui n'aura subi aucun set depuis la création renverra l'article par défaut.

Cette valeur par défaut nous est fournie par le constructeur make :

   let make x =
      {plus = Leaf; minus = Leaf; default = x}

Pour accéder à un article à partir de son indice :

• on distingue les indices positifs ou nuls des indices strictement négatifs ;
• selon le cas on choisit la racine plus ou la racine minus ;
• lorsqu'on a atteint une feuille, cela signifie que l'indice n'a jamais fait l'objet d'un set, on renvoie l'article par défaut ;
• sinon on a affaire à un nœud ;
• si l'indice vaut 1 on renvoie l'article contenu dans ce nœud ;
• on poursuit dans l'arbre à gauche (respectivement à droite) si l'indice est pair (respectivement impair) ;
• on divise l'indice par 2.

    let get v i =
      let rec loop i node =
        match node with
        | Leaf ->
            v.default
        | Node n ->
            if i = 1 then n.item else
            loop (i asr 1) (if i land 1 = 0 then n.left else n.right)
      in if i >= 0 then loop (succ i) v.plus else loop (-i) v.minus

Pour modifier l'article situé à un certain indice :

• on distingue les indices positifs ou nuls des indices strictement négatifs ;
• selon le cas on choisit la racine plus ou la racine minus ;
• on parcourt l'arbre jusqu'à trouver le nœud d'indice recherché, on modifie son item ;
• si on atteint une feuille alors, l'indice n'est pas présent, dans ce cas il va falloir faire bourgeonner cette feuille en une nouvelle branche jusqu'à atteindre l'indice recherché pour y déposer l'article voulu.

    let set v i x =
      let rec grow i =
        Node
        (
        if i = 1 then
          {left = Leaf; item = x; right = Leaf}
        else if i land 1 = 0 then
          {left = grow (i asr 1); item = v.default; right = Leaf}
        else
          {left = Leaf; item = v.default; right = grow (i asr 1)}
        )
      and tree i node =
        match node with
        | Leaf ->
            grow i
        | Node n ->
            if i = 1 then
              n.item <- x
            else if i land 1 = 0 then
              n.left <- tree (i asr 1) n.left
            else
              n.right <- tree (i asr 1) n.right;
            node
      in
      if i >= 0 then
        v.plus <- tree (succ i) v.plus
      else
        v.minus <- tree (-i) v.minus

L'arbre de Braun est simple à implémenter, beaucoup plus facile que l'arbre AVL, il n'y a pas de rotations et les nœuds sont très légers, ils ne stockent pas de clé et ils ne contiennent aucune information sur l'équilibre/déséquilibre des deux sous-arbres.
De plus le temps d'accès est directement proportionnel à la longueur de la clé tandis que, dans le cas général, la performance d'un arbre AVL sera affectée à la fois par la longueur de la clé et par le nombre d'éléments déjà présents.

Nous verrons toutefois au chapitre suivant que cette performance a un prix.

En attendant, nous pouvons implémenter une optimisation assez élémentaire.
Telle que la fonction set est codée, l'assignation de l'article par défaut ne provoque jamais la libération d'aucun nœud.
La modification de la fonction set, de façon à permettre la décroissance de l'arbre de Braun lorsque l'article par défaut est assigné à une feuille, ne nécessite que l'insertion de deux lignes supplémentaires (que l'on a coloriées en vert) :

    let set v i x =
      let rec grow i =
        Node
        (
        if i = 1 then
          {left = Leaf; item = x; right = Leaf}
        else if i land 1 = 0 then
          {left = grow (i asr 1); item = v.default; right = Leaf}
        else
          {left = Leaf; item = v.default; right = grow (i asr 1)}
        )
      and tree i node =
        match node with
        | Leaf ->
            grow i
        | Node n ->
            if i = 1 then
              n.item <- x
            else if i land 1 = 0 then
              n.left <- tree (i asr 1) n.left
            else
              n.right <- tree (i asr 1) n.right;
            if x = v.default && n.left = Leaf && n.right = Leaf then Leaf
            else node
      in
      if i >= 0 then
        v.plus <- tree (succ i) v.plus
      else
        v.minus <- tree (-i) v.minus

Pour ceux qui préféreraient une version immutable de ce TAD, il suffit d'opter pour une fonction d'ajout appropriée, qui opère une copie de la partie de l'arbre altérée par l'opération d'insertion :

    let add v i x =
      let rec grow i =
        Node
        (
        if i = 1 then
          {left = Leaf; item = x; right = Leaf}
        else if i land 1 = 0 then
          {left = grow (i asr 1); item = v.default; right = Leaf}
        else
          {left = Leaf; item = v.default; right = grow (i asr 1)}
        )
      and tree i node =
        match node with
        | Leaf ->
            grow i
        | Node n ->
            Node
            (
            if i = 1 then
              {n with item = x}
            else if i land 1 = 0 then
              {n with left = tree (i asr 1) n.left}
            else
              {n with right = tree (i asr 1) n.right}
            )    
      in
      if i >= 0 then
        {v with plus = tree (succ i) v.plus}
      else
        {v with minus = tree (-i) v.minus; plus = v.plus}

On ne peut s'empêcher de remarquer la grande similitude entre la version mutable et la version immutable.
C'est parce que l'algorithme est le même, seul le moyen change, l'affectation r.a <- b est remplacée par l'expression {r with a = b} :

• l'assignation r.a <- b modifie sur place le champ a en lui affectant la valeur b ;
• l'opération {r with a = b} renvoie une copie de l'enregistrement r dans laquelle le champ a a pour valeur b.

Cependant, add ne suffit pas à rendre le TAD définitivement immutable, pour cela il faudrait carrément retirer les mots-clés mutable dans le type 'a node.

Mais c'est tout de même un compromis acceptable entre deux écueils possibles :

• un TAD immutable qui sollicite trop le ramasse-miettes parce que dans l'usage qu'on en fait toutes les modifications pourraient se faire sur place ;
• un TAD mutable que l'on utilise comme un TAD fonctionnel, si bien qu'il n'est impur que par péché.

Afin de faciliter vos expérimentations, la source complète du module Vector a été archivée ici.

La figure ci-dessous représente les indices des nœuds dans un arbre de Braun, en notation décimale cette fois-ci.

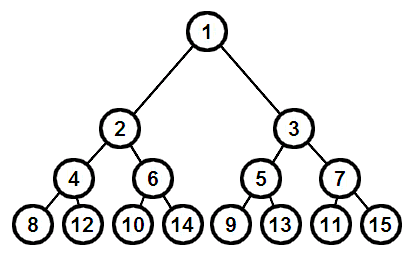
Il ne sera pas facile de parcourir l'arbre de telle façon de que nous traversions les indices dans l'ordre, qu'il soit croissant ou décroissant.
De plus la relation entre l'indice et la position dans l'arbre n'est pas la même pour la moitié positive et pour la moitié négative.
Et nous avons plus d'un itérateur à coder.

Tout cela ne nous facilite pas la tâche et pourrait impliquer plus de travail que nous l'envisagions au départ.

Une astuce pour minimiser l'effort consiste à maximiser la réutilisation interne en codant les fonctions courantes à partir des fonctions les plus générales :

    let map f v =
      mapi (fun i -> f) v

    let iter f v = 
      fold (fun h t -> f h) () v

    let exists p v = 
      fold (fun h t -> p h or t) false v

    let for_all p v = 
      fold (fun h t -> p h && t) true v

    let filter p v =
      fold (fun h t -> if p v then h::t else t) [] v

    let to_list v =
      fold (fun h t -> h::t) [] v

    let iteri f v = 
      foldi (fun i h t -> f i h) () v

    let to_alist v =
      foldi (fun i h t -> (i,h)::t) [] v

De cette façon il ne nous reste plus qu'à coder fold, foldi et mapi.

Mais avant il nous faut choisir une façon de relier l'indice et l'ordre d'application dans fold.
Nous choisissons de ne pas les relier.
Le choix contraire nous aurait fait regretter l'arbre AVL qui aurait été plus avantageux quant à la traversée selon les indices.

Commençons par le fold. Pour une feuille on retourne l'accumulateur, pour un nœud :

1. on parcourt l'arbre gauche ;
2. on applique f avec l'article de ce nœud et (1) pour arguments ;
3. on parcourt l'arbre droit, avec (2) pour valeur initiale.

    let fold f init v =
      let rec loop node acc =
        match node with
        | Leaf ->
            acc
        | Node n -> 
            if n.item = v.default then loop n.right (loop n.left acc)
            else loop n.right (f n.item (loop n.left acc))
      in loop v.plus (loop v.minus init)

La figure ci-dessous montre comment calculer les indices, de façon incrémentale à partir de la racine.

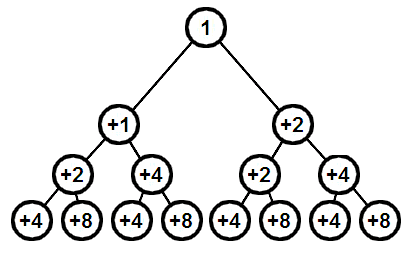
Ce qu'il faut en retenir c'est que :

• pour un fils à droite il faut ajouter le nombre de nœuds que peut contenir le niveau actuel ;
• pour un fils à gauche il faut ajouter le nombre de nœuds que peut contenir le niveau supérieur.

Cela nous fournit l'indication qui nous manquait pour le calcul des indices dans foldi.

    let foldi f init v =
      let rec plus node i d acc =
        match node with
        | Leaf ->
            acc
        | Node n -> 
            let middle = plus n.left (i+d) (d+d) acc in
            plus n.right (i+d+d) (d+d)
            (if n.item = v.default then middle else (f (i-1) n.item middle))
      and minus node i d acc =
        match node with
        | Leaf ->
            acc
        | Node n -> 
            let middle = minus n.right (i+d+d) (d+d) acc in
            minus n.left (i+d) (d+d)
            (if n.item = v.default then middle else (f (-i) n.item middle))
      in plus v.plus 1 1 (minus v.minus 1 1 init)

Comme nous l'avions anticipé, il faut dédoubler la routine de parcours, car le calcul n'est pas le même pour les indices positifs et pour les indices négatifs.

Ce dédoublement affecte tout autant la fonction mapi, que nous ne pouvons pas coder à l'aide de foldi puisque nous devons reproduire la structure (l'arbre de Braun) alors que notre fold se contente d'en énumérer chaque élément.

    let mapi f v =
      let rec plus node i d =
        match node with
        | Leaf ->
            Leaf
        | Node n -> 
            Node
            {
            left  = plus n.left (i+d) (d+d);
            item  = f (i-1) n.item;
            right = plus n.right (i+d+d) (d+d);
            }
      and minus node i d =
        match node with
        | Leaf ->
            Leaf
        | Node n -> 
            Node
            {
            left  = minus n.left (i+d) (d+d);
            item  = f (-i) n.item;
            right = minus n.right (i+d+d) (d+d);
            }
      in {plus = plus v.plus 1 1; minus = minus v.minus 1 1; default = f v.default}